A descoberta da Divina Proporção, Regra de Ouro ou Proporção Áurea é resultado da busca pela beleza nas formas. Os gregos eram apaixonados pelas formas e procuraram dar sentido a tudo que existia e tudo que faziam, buscando proporções a partir da Natureza, “Pitágoras (569 – 500 a.C.) (…) observou a ocorrência, na Natureza, de certas combinações e relações entre números.” Huntley (1985, p. 35). Ele acreditava que: Idem, “a explicação da ordem e da harmonia na Natureza iria ser encontrada na ciência dos números.” É possível que a Divina Proporção esteja a ser usada a pelo menos 4.000 anos. Ao longo da história pode ser observada em diferentes áreas, desde na música, para obter resultados mais harmónicos, na arquitectura, no design e na arte.
A letra grega da Razão Áurea (?)
A letra grega que designa a Razão Áurea é Fi (?), letra inicial de Fídias, um importante escultor grego, autor de umas das mais conhecidas estátuas da antiguidade; a Atena Partenos e o Zeus Olímpico. “Em 1509 foi publicado um tratado de Luca Pacioli, De Divina Proportione, ilustrado por Leonardo da Vinci. Reproduzido em 1956 em uma vistosa edição, é um compêndio fascinante da aparição do fi em várias figuras sólidas.” HUNTLEY (1985: 37) O Fi corresponde, aproximadamente a 1, 618. Os egípcios, também usaram esses conhecimentos nas suas construções, especialmente nas pirâmides; as pedras usadas em suas construções seguiam uma proporção constante, cada pedra era 1, 618 menor do que a pedra que estivesse a baixo. Usaram esses conhecimentos, também em templos e sepulcros, pois acreditavam que se assim não fosse, seus deuses não iriam gostar e as almas dos mortos não seguiria o seu destino.
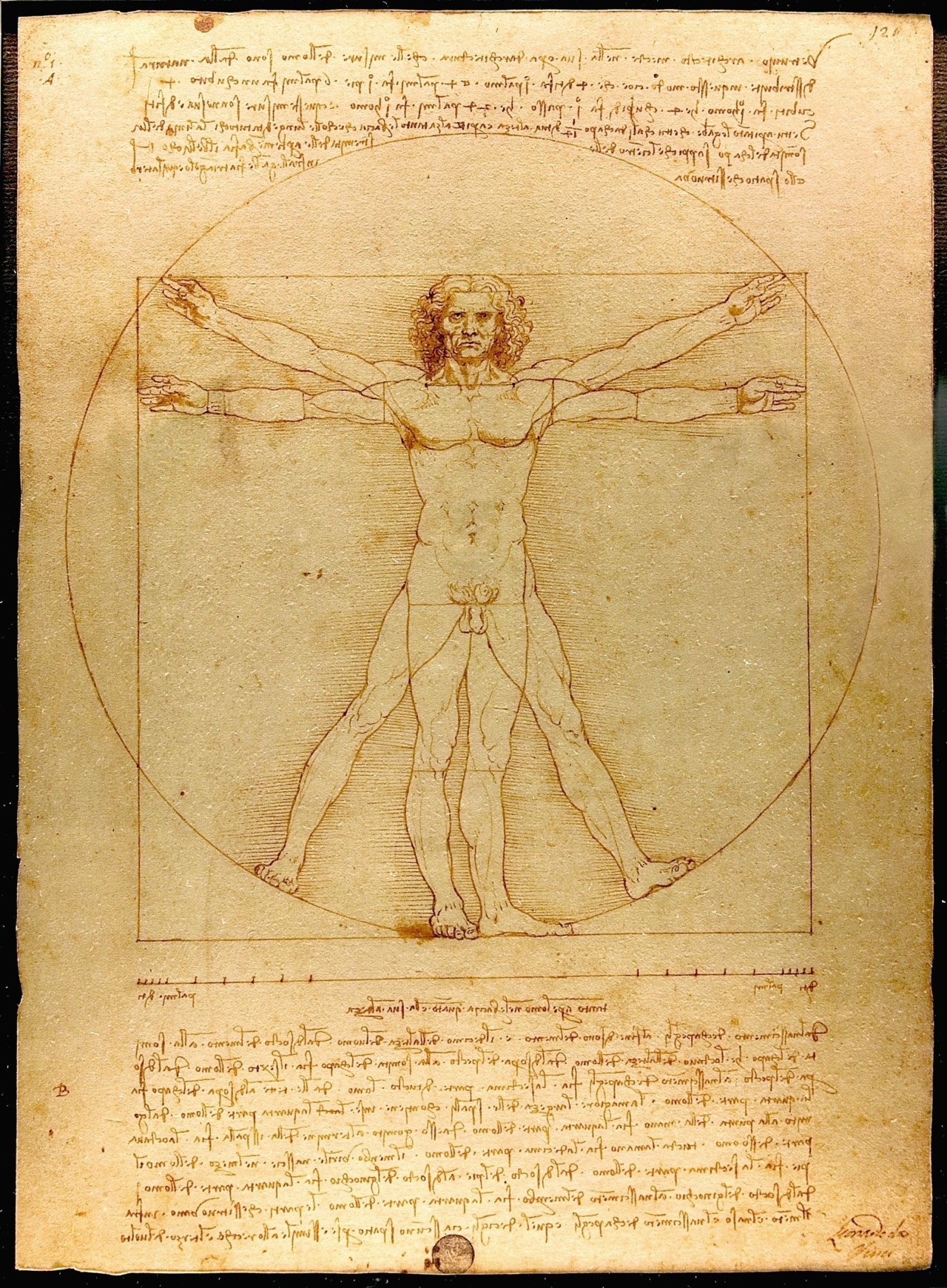
Leonardo da Vinci afirmava que, “no Homem perfeito, as dimensões obedecem a proporção áurea.” (www.designculture.com.br)
“É uma pena que a divisão áurea tenha atraído a entusiástica atenção dos excêntricos. Um deles mediu as alturas de 65 mulheres e comparou os resultados com as alturas de seus respectivos umbigos, tendo obtido a média de 1, 618.” (Huntley, 1985, p. 37)
Vários outros estudos foram feitos, e mais descobertas vieram a tona sobre a número de ouro:
“ – A proporção de abelhas fêmeas em comparação com abelhas machos numa colmeia é de 1,618.
– A proporção que aumenta o tamanho das espirais de um caracol é de 1,618.
– A proporção em que aumenta o diâmetro das espirais sementes de um girassol é de 1,618.
– A proporção em que diminuem as folhas de uma árvore à medida que subimos é de 1,618.
– As estrelas distribuem-se perante um astro principal numa espiral obedecendo à proporção de 1,618.” (www.designculture.com.br)
Entre 570 e 500 a.C., Pitágoras descobriu que as proporções do pentagrama eram áureas, e o pentagrama foi transformado no símbolo da Irmandade Pitagórica.
“Um outro facto familiar à escola de Pitágoras era há cinco, e somente cinco sólidos convexos regulares que podem, cada um, ser circunscritos por uma esfera: o tetraedro, o cubo, o octaedro, o icosaedro, e o dodecaedro. Um gosto pelos “mistérios” levou os gregos antigos a atribuir um significado especial ao último deles: suas doze facetas regulares correspondiam aos doze signos do zodíaco. Era um símbolo do universo. Mais que isso, cada face pentagonal, associada à divisão áurea, era de um interesse especial para os pitagóricos. O ponto de intersecção P de duas diagonais divide cada uma delas na proporção áurea.” (Huntley, 1985)
Leonardo da Vinci, aplicou os conhecimentos sobre a divina proporção no conhecido “Home Vitruviano”, apresentando as proporções exactas da anatomia do Homem.
A Sequência de Fibonacci (Fi-Bonacci)
Idem, “(…) há uma série somatória – e somente uma – que proporciona encaixe exacto. É uma série que utiliza a divisão áurea. Ela pode adequadamente chamada série áurea”
A Sequência de Fibonacci resume-se na lei de que: cada termo é resultado da soma dos dois anteriores. A razão entre o termo posterior com um termo anterior resulta num valor próximo ao número de ouro (?).
Leonardo Fibonacci (1180 – 1250) procurou explicar a reprodução de coelhos, através de uma seguência que mantinha uma proporção; “Um casal de coelhos atinge a maturidade sexual em dois meses, a cada mês, um casal com maturidade sexual gera um novo casal. Considerando que as condições desses coelhos sejam iguais e ignorando qualquer problema genético, quantos coelhos teremos em N meses?
A resposta é dada pela sequência, considerando cada mês a quantidade de casais, 1,,1,2,3,5,8,13,21,34,55,…” (www.portillodesign.com.br)
Dada pela fórmula: Fn = Fn-1 + Fn – 2.
3/2 = 1,5 ; 5/3 = 1, 666… ; 8/5 = 1, 6 ; 13/8 = 1, 625 ; 21/13 = 1, 615…
O Rectângulo de Ouro
“O rectângulo cujos lados adjacentes têm comprimentos em razão que aproxima – se ou é exactamente igual a ?:1 parece proporcionar uma medida maior de satisfação para um número maior de pessoas que os rectângulos de proporções diferentes” (Huntley, 1985, p. 57)
Esse rectângulo chama-se rectângulo de ouro, ou simplesmente rectângulo áureo, cujos comprimentos AB:AD = ?; designado por Huntley (1985), como “fonte de prazer”. Apresenta-se mais harmónico e com maior facilidade é aceite pelo nosso cérebro. Idem, “(…) exerce apelo sobre a população maior que a de um rectângulo de qualquer formato.” O Partenon, em Atenas, no século V a.C., a célebre obra “A Última Ceia”, de Leonardo da Vinci, são exemplos conhecidos que se encaixam no rectângulo áureo.

Em todos os tempos o rectângulo áureo mostrou-se eficaz e harmonioso, para além de ser aplicado em objectos do dia-a-dia e muitas poucas vazes notamos que, esta presente o rectângulo de ouro. As vezes os objectos podem parecer desconfortáveis ou simplesmente diferentes quando não se enquadrarem na “divina proporção”.
Idem, “Fechner fez literalmente, milhares de mensurações da razão de rectângulos que são vistos comumente – cartas de baralho, janelas, blocos de papel de carta, capas de livros- e descobriu que a média aproximava-se do fi. Ele também testou preferências pessoais extensivamente e finalmente determinou que a maioria das pessoas prefere um certo rectângulo cujas proporções estão entre as do quadrado e as do duplo quadrado”
O rectângulo de ouro é “(…) útil, económico e agradável, pois não difere seriamente em formato do rectângulo áureo, que é familiar para o olho do artista” (Idem), do arquitecto e do designer.
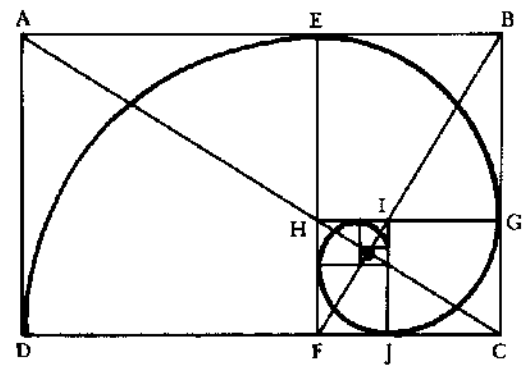
A Espiral de Ouro
Uma das mais harmónicas curvas, conhecidas em geometria é a espiral de ouro, também designada espiral logarítmica ou espiral equiangular. “Verificamos que essas espirais têm sido ocorrência comum no mundo natural durante milhões de anos.” (Huntley, 1985, p. 99) A espiral logarítmica é, claramente mais um símbolo da estética e beleza.
Idem, “Esta elegante espiral fará apelo primeiro às nossas sensibilidades artísticas e somente depois à nossa sofisticada apreciação matemática. Imagina-se se este apelo prévio do formato da curva estaria relacionado ao facto de este ter sido uma paisagem familiar no mundo da natureza a partir do momento que houve homens para vê-lo.
As diagonais por onde passa a espiral são opostas, os comprimentos dos quadros sucessivos formam a sequência de Fibonacci, por mais que a espiral logarítmica cresça, para fora ou dentro do rectângulo áureo, o seu formato não muda (ver figura 8).
Idem, “As câmaras sucessivas da concha de náutilo (frontispício) estão construídas sobre estrutura de uma espiral logarítmica. À medida que a concha cresce, o tamanho das câmaras aumenta mas seu tamanho permanece inalterado.”
A Divina Proporção Aplicada ao Design Gráfico
O Design Gráfico moderno recorre frequentemente à divina proporção; o rectângulo áureo, o pentagrama, a espiral logarítmica e a sequência de Fibonacci tem sido recursos importantes na concepção de projectos de design, no geral.
“No design gráfico, a espiral de Fibonacci talvez seja a forma mais usada para criar uma leitura mais fluida dos elementos da imagem. Na diagramação de livros, por exemplo o uso de rectângulos áureos são usados para criar um espaçamento entre bordas mais confortáveis para a leitura” (www.portillodesign.com.br)
Outros projectos, em diferentes campos do Design Gráfico, usam a divina proporção para alcançar resultados mais harmónicos e persuasivos, resultados mais atractivos e visualmente convicentes. Os produtos da Apple são exemplos modernos do uso da espiral de logarítmica. A divina proporção é aplicada na criação de tipografias e desenho de ícones.
As proporções entre títulos de jornais ou revistas podem ser obtidas recorrendo a sequência de Fibonacci. Actualmente, estudos mostram que é possível aplicar conhecimentos sobre a divina proporção, também nas cores, com base na sua frequência, que é determinada em valores numéricos, e, que aos serem colocadas em sequência são obtidas combinações mais agradáveis.
Os designers, actualmente, com conhecimento da divina proporção, encontram extraordinários resultados, mesmo inconscientemente, com a experiência, procuram o máximo de equilíbrio em seus projectos, e por isso quando estudados é encontrado um equilíbrio que se sustenta na divina proporção, e por isso apresentam-se mais atractivos comparados com os outros. Os cartões feitos sob um formato igual ou próximo ao rectângulo de ouro apresentam maior conforto, e as pessoas tem sido mais simpáticas a estes. A proporção áurea é igualmente aplicada na concepção, não apenas dos formatos mas também no design de cartazes publicitários.
Fonte: TINGA, Mélio Estratégias Persuasivas Aplicadas na Concepção Visual de Cartaz Publicitário, Trabalho de conclusão de curso. Universidade Pedagógica. 2017. 140p.



